A four- vector is a quantity with four components which changes like spacetime coordinates under a coordinate transformation. We will write the displacement four- vector as:
is a frame independent vector joining near by
points in spacetime. 
means: has components in
frame 
. 
are the coordinates themselves
[ which are coordinate dependent ].
In frame 
, the coordinates are
so:
The Lorentz transformations can be written as
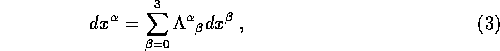
where 
is the 
Lorentz transformation matrix
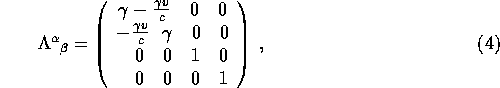
and
, can be regarded
as column vectors.
The positioning of the indices is explained later but indicates that we can use the summation convention: sum over repeated indices, if one index is up and one index down. Thus we can write:
is a dummy- index which can be
replaced by any other index;
is a free- index , so the
above equation is equivalent to four equations. For a general four- vector
we can write
If 
and 
are two four- vectors, clearly
and
are also four- vectors with
obvious components
and
In any frame we can define a set of four- basis
vectors :
and
In general we can write
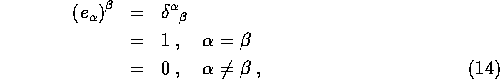
where 
labels the basis vector and labels the
coordinate.
Any four- vector can be expressed as a sum of four- vectors parallel to the basis vectors i.e.
The last equality reflects the fact that four- vectors are frame independent.
Writing:
where we have exchanged the dummy indices and
and and 
, we see that this equals
for all if and only if
This gives the transformation law for basis vectors :
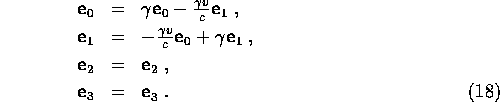
Note that the basis transformation law is different from the
transformation law for the components since 
takes one from frame to .
So in summary, for vector basis and vector components we have:
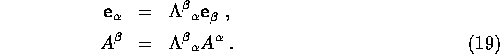
Since has a velocity 
relative to
, we have:
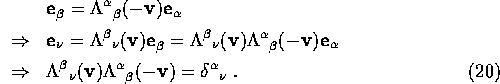
So 
is the
inverse of
.
Likewise
It follows that the Lorentz transformations with gives the
components of a four- vector in from those in .
The magnitude of a four- vector
is defined as 
:
in analogy with the line element
The sign on the 
will be explained later. This is a frame
invariant scalar.
is spacelike if
, timelike if
and null if 
.
The scalar product
of two four- vectors and is:
Since
is frame independent.
and are orthogonal if
; they are not necessarily
perpendicular in the spacetime diagram [ for example a null vector is
orthogonal to itself ], but must make equal angles with the
line.
Basis vectors form an orthonormal tetrad since they are orthogonal:
if 
, normalized
to unit magnitude: 
:
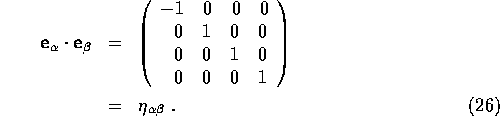
We will see later what the geometrical significance of
is.